poyadvance.blogg.se

Thus, we obtain the following estimate of σ b1.įor Armand’s Pizza Parlors, s = 13.829.

Note that the expected value of b 1 is equal to β 1, so b 1 is an unbiased estimator of β 1.īecause we do not know the value of s, we develop an estimate of σ b, denoted σ b1, by estimating σ with s in equation (14.17). The properties of the sampling distribution of b 1 follow. Indeed, b 0 and b 1, the least squares estimators, are sample statistics with their own sampling distributions. However, it is doubtful that we would obtain exactly the same equation (with an intercept of exactly 60 and a slope of exactly 5). A regression analysis of this new sample might result in an estimated regression equation similar to our previous estimated regres­sion equation y = 60 + 5x. For example, suppose that Armand’s Pizza Parlors used the sales records of a different sample of 10 restaurants. The properties of the sampling distribution of b 1, the least squares estimator of β 1, provide the basis for the hypothesis test.įirst, let us consider what would happen if we used a different random sample for the same regression study. However, if H 0 cannot be rejected, we will have insufficient evidence to conclude that a significant relationship exists.

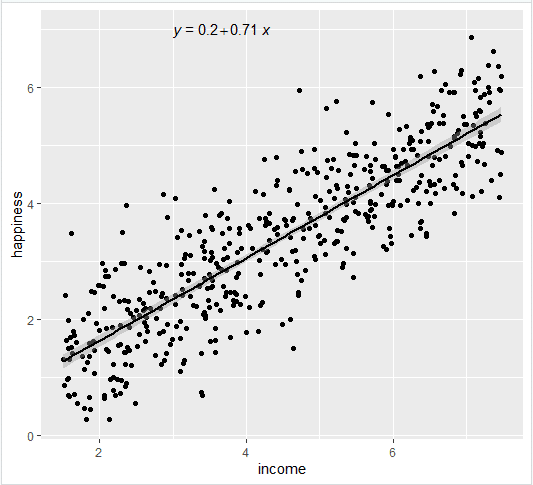
If H 0 is rejected, we will conclude that β 1 # 0 and that a statistically significant rela­tionship exists between the two variables. We will use the sample data to test the following hypotheses about the para­meter β 1. The purpose of the t test is to see whether we can conclude that β 1 # 0. If x and y are linearly related, we must have β 1 # 0. The simple linear regression model is y = β 0 + β1 x + ∈. In the fol­lowing discussion, we use the standard error of the estimate in the tests for a significant relationship between x and y. The resulting value, s, is referred to as the standard error of the estimate.įor the Armand’s Pizza Parlors example, s = VMSE = V191.25 = 13.829. To estimate a we take the square root of s 2. In Section 14.3 we showed that for the Armand’s Pizza Parlors example, SSE = 1530 hence, Because the value of MSE provides an estimate of a 2, the notation s 2 is also used. MSE provides an unbiased estimator of σ 2. Thus, the mean square error is computed by dividing SSE by n – 2. Statisticians have shown that SSE has n – 2 degrees of freedom because two parameters (β 0 and β 1) must be estimated to compute SSE. The mean square error (MSE) provides the estimate of σ 2 it is SSE divided by its degrees of freedom.Įvery sum of squares has associated with it a number called its degrees of freedom. Thus, SSE, the sum of squared residuals, is a measure of the variability of the actual observations about the estimated regression line. Recall that the deviations of the y values about the estimated regression line are called residuals. Estimate of σ 2įrom the regression model and its assumptions we can conclude that σ 2, the variance of e, also represents the variance of the y values about the regression line.

Both require an estimate of σ 2, the variance of e in the regression model. Thus, to test for a significant regression relationship, we must conduct a hypothesis test to determine whether the value of β 1 is zero. Alternatively, if the value of β 1 is not equal to zero, we would conclude that the two variables are related. In this case, the mean value of y does not depend on the value of x and hence we would conclude that x and y are not linearly related. If the value of β 1 is zero, E(y) = β 0 + (0)x = b 0. To establish the simplest typical regression model, we set following four assumptions for the regression model with the acronym ‘LINE’.In a simple linear regression equation, the mean or expected value of y is a linear func­tion of x: E(y) = β 0 + β 1x. The regression model has been developed as a typical statistical model based on the idea by Francis Galton in 1886. In the regression model the values on the line is considered as the mean of Y corresponding to each X value and we call the Y values on the line as Ŷ (Y hat), the predicted Y values.

We call this model as a ‘regression model’ and especially a ‘simple linear regression model’ when only one X variable is included. Therefore, individual data points can have some distances from the straight line by various amounts of deviations from their means. Subgroups of X have certain distributions around their means, e.g., normal distribution. Why do we try to express the scattered data points as a straight line? The main idea is that the line represents means of Y for subgroups of X, not individual data points ( Figure 1B). (A) Description of relationship of 2 variables, X and Y (B) A conceptual relationship between the regression line and surrounding subgroups in the regression model.